Pecahan merupakan salah satu konsep matematika fundamental yang akan terus menemani siswa di jenjang pendidikan selanjutnya. Di kelas 4 SD, pemahaman yang kuat tentang pecahan menjadi kunci untuk membuka pintu ke berbagai topik matematika yang lebih kompleks, mulai dari operasi hitung pecahan, desimal, hingga persentase. Namun, bagi sebagian siswa, konsep pecahan terkadang terasa membingungkan. Untuk mengatasi hal ini, latihan soal yang variatif dan terstruktur menjadi sangat penting.

Artikel ini hadir untuk membantu para siswa kelas 4 SD dalam menguasai konsep pecahan melalui kumpulan soal latihan yang dirancang khusus. Kita akan menjelajahi berbagai aspek pecahan, mulai dari pengenalan, membandingkan, menjumlahkan, mengurangkan, hingga mengalikan pecahan sederhana. Mari kita mulai perjalanan menyenangkan ini untuk menaklukkan dunia pecahan!

Bagian 1: Memahami Dasar-Dasar Pecahan

Sebelum melangkah ke soal-soal yang lebih menantang, penting untuk memastikan pemahaman dasar tentang apa itu pecahan. Pecahan merepresentasikan bagian dari keseluruhan. Bentuk umumnya adalah $fracab$, di mana $a$ disebut pembilang (angka di atas garis) dan $b$ disebut penyebut (angka di bawah garis). Pembilang menunjukkan berapa banyak bagian yang kita miliki, sementara penyebut menunjukkan berapa banyak bagian total dari keseluruhan tersebut.

Contoh: Jika sebuah pizza dipotong menjadi 8 bagian yang sama, dan Anda makan 3 potong, maka Anda makan $frac38$ bagian dari pizza tersebut. Di sini, 3 adalah pembilang dan 8 adalah penyebut.

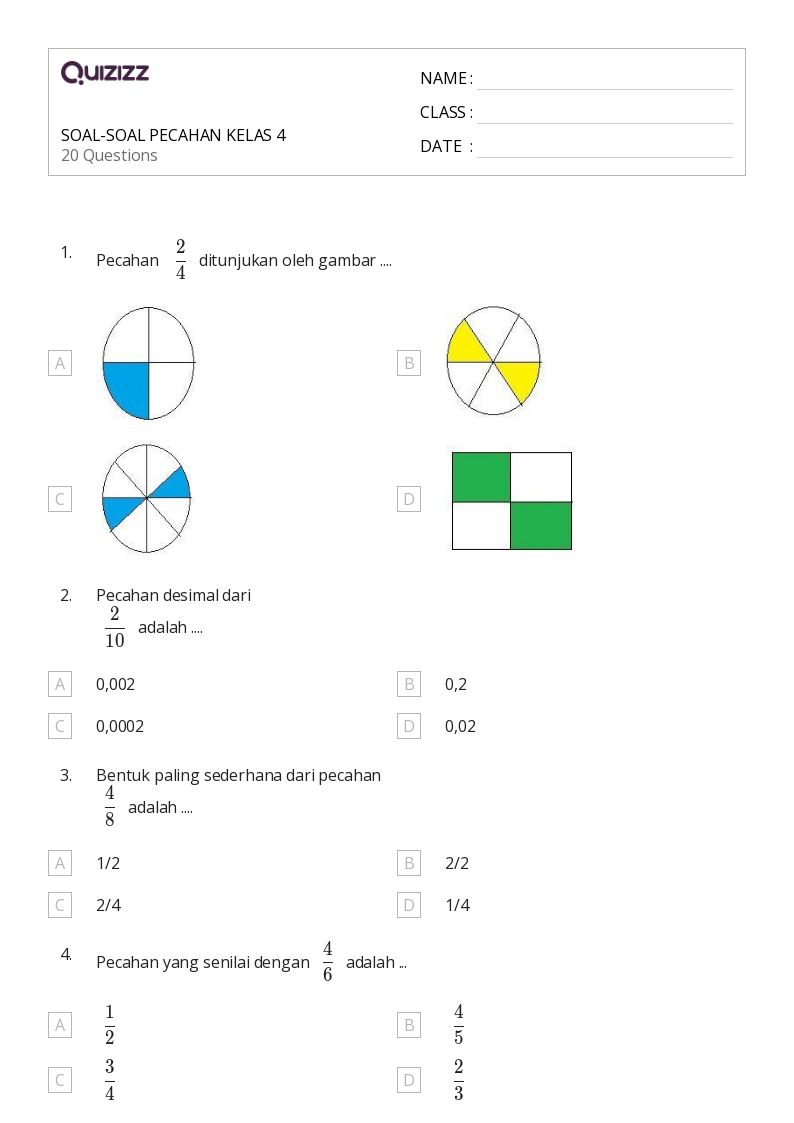
Soal Latihan 1: Identifikasi Pecahan

1. Gambar sebuah lingkaran dan bagi menjadi 4 bagian yang sama. Warnai 1 bagian. Pecahan berapa yang diwarnai?
2. Seorang guru membagikan 10 pensil kepada 5 siswa secara merata. Berapa bagian pensil yang diterima setiap siswa? Tuliskan dalam bentuk pecahan.
3. Dalam sebuah keranjang terdapat 12 buah apel. 5 buah apel sudah dimakan. Berapa bagian apel yang tersisa?
4. Tuliskan pecahan yang menyatakan bagian yang diarsir dari bangun datar berikut:
   • Persegi panjang dibagi 6 kotak, 2 kotak diarsir.
   • Segitiga dibagi 3 bagian sama besar, 1 bagian diarsir.
   • Lingkaran dibagi 8 juring, 5 juring diarsir.
5. Jelaskan apa arti dari pecahan $frac25$?

Bagian 2: Pecahan Senilai

Pecahan senilai adalah pecahan-pecahan yang memiliki nilai yang sama, meskipun pembilang dan penyebutnya berbeda. Kita dapat menemukan pecahan senilai dengan mengalikan atau membagi pembilang dan penyebut dengan bilangan yang sama (bukan nol).

Contoh: $frac12$ senilai dengan $frac24$, $frac36$, dan seterusnya. Jika kita punya $frac12$ liter susu, itu sama saja dengan $frac24$ liter susu.

Soal Latihan 2: Mencari Pecahan Senilai

1. Temukan dua pecahan yang senilai dengan $frac13$.
2. Temukan tiga pecahan yang senilai dengan $frac34$.
3. Lingkari pecahan-pecahan yang senilai dengan $frac25$: $frac410$, $frac615$, $frac310$, $frac820$.
4. Sederhanakan pecahan $frac1218$ menjadi pecahan senilai yang paling sederhana. (Petunjuk: bagi pembilang dan penyebut dengan FPB-nya).
5. Lengkapi pecahan berikut agar menjadi pecahan senilai:
   • $frac23 = frac?6$
   • $frac35 = frac9?$
   • $frac1015 = frac?3$

Bagian 3: Membandingkan Pecahan

Membandingkan pecahan membantu kita menentukan pecahan mana yang lebih besar atau lebih kecil. Ada beberapa cara untuk membandingkan pecahan:

• Jika penyebutnya sama: Bandingkan pembilangnya. Pecahan dengan pembilang yang lebih besar adalah pecahan yang lebih besar.
• Jika pembilangnya sama: Bandingkan penyebutnya. Pecahan dengan penyebut yang lebih kecil adalah pecahan yang lebih besar (karena bagiannya dibagi menjadi lebih sedikit).
• Menyamakan penyebut: Ubah pecahan menjadi pecahan senilai dengan penyebut yang sama, lalu bandingkan pembilangnya.

Contoh: Membandingkan $frac25$ dan $frac35$. Karena penyebutnya sama (5), kita bandingkan pembilangnya (2 dan 3). Karena 3 lebih besar dari 2, maka $frac35$ lebih besar dari $frac25$.

Soal Latihan 3: Membandingkan Pecahan

1. Urutkan pecahan berikut dari yang terkecil hingga terbesar: $frac37$, $frac57$, $frac17$, $frac47$.
2. Urutkan pecahan berikut dari yang terbesar hingga terkecil: $frac29$, $frac79$, $frac59$, $frac19$.
3. Bandingkan pecahan berikut menggunakan tanda $<$ (lebih kecil dari), $>$ (lebih besar dari), atau $=$ (sama dengan):
   • $frac38$ ___ $frac58$
   • $frac610$ ___ $frac410$
   • $frac12$ ___ $frac14$
   • $frac23$ ___ $frac25$
4. Bandingkan pecahan $frac23$ dan $frac34$. Gunakan cara menyamakan penyebut. Pecahan mana yang lebih besar?
5. Ani memiliki pita sepanjang $frac35$ meter. Budi memiliki pita sepanjang $frac23$ meter. Siapa yang memiliki pita lebih panjang?

Bagian 4: Menjumlahkan dan Mengurangkan Pecahan

Menjumlahkan dan mengurangkan pecahan menjadi lebih mudah jika penyebutnya sama.

• Jika penyebutnya sama: Jumlahkan atau kurangkan pembilangnya, sementara penyebutnya tetap sama.
• Jika penyebutnya berbeda: Samakan dulu penyebutnya dengan mencari KPK dari kedua penyebut, lalu ubah kedua pecahan menjadi pecahan senilai dengan penyebut yang sama. Setelah penyebutnya sama, baru lakukan penjumlahan atau pengurangan.

Contoh:

• $frac15 + frac25 = frac1+25 = frac35$
• $frac47 – frac17 = frac4-17 = frac37$
• $frac12 + frac14$. KPK dari 2 dan 4 adalah 4. Maka, $frac12 = frac24$. Jadi, $frac24 + frac14 = frac2+14 = frac34$.

Soal Latihan 4: Penjumlahan dan Pengurangan Pecahan

1. Hitunglah:
   • $frac26 + frac36$
   • $frac79 – frac49$
   • $frac13 + frac13$
   • $frac58 – frac28$
2. Hitunglah:
   • $frac12 + frac13$
   • $frac25 + frac110$
   • $frac34 – frac12$
   • $frac56 – frac13$
3. Ibu membeli $frac34$ kg gula. Ibu menggunakan $frac14$ kg gula untuk membuat kue. Berapa sisa gula ibu sekarang?
4. Dalam sebuah botol berisi air $frac710$ liter. Dituangkan $frac35$ liter air ke dalam gelas. Berapa sisa air dalam botol?
5. Ayah membaca buku cerita sebanyak $frac25$ bagian pada hari Sabtu dan $frac310$ bagian pada hari Minggu. Berapa total bagian buku yang dibaca ayah pada akhir pekan?

Bagian 5: Mengalikan Pecahan Sederhana

Mengalikan pecahan pada dasarnya adalah mengalikan pembilang dengan pembilang dan penyebut dengan penyebut.

• Pecahan dikali Pecahan: $fracab times fraccd = fraca times cb times d$
• Pecahan dikali Bilangan Bulat: Menganggap bilangan bulat sebagai pecahan dengan penyebut 1. Misalnya, $3 times frac12 = frac31 times frac12 = frac3 times 11 times 2 = frac32$.

Contoh:

• $frac13 times frac25 = frac1 times 23 times 5 = frac215$
• $4 times frac13 = frac41 times frac13 = frac4 times 11 times 3 = frac43$

Soal Latihan 5: Perkalian Pecahan

1. Hitunglah:
   • $frac14 times frac35$
   • $frac27 times frac13$
   • $frac38 times frac25$
2. Hitunglah perkalian bilangan bulat dengan pecahan:
   • $5 times frac12$
   • $3 times frac27$
   • $6 times frac14$
3. Kakak memiliki $frac34$ bagian dari sebuah kue. Kakak memberikan $frac12$ bagian dari sisa kue tersebut kepada adiknya. Berapa bagian kue yang diberikan kakak kepada adiknya?
4. Dalam sebuah wadah terdapat $frac23$ liter air. Air tersebut akan dimasukkan ke dalam gelas yang masing-masing berukuran $frac16$ liter. Berapa gelas yang bisa terisi penuh?
5. Sebuah kebun memiliki luas $frac58$ hektar. Sebanyak $frac13$ bagian dari kebun tersebut ditanami jagung. Berapa hektar luas kebun yang ditanami jagung?

Penutup

Menguasai konsep pecahan membutuhkan latihan yang konsisten. Dengan mengerjakan berbagai jenis soal seperti yang disajikan di atas, siswa kelas 4 SD diharapkan dapat membangun kepercayaan diri dan pemahaman yang kokoh. Ingatlah bahwa kesalahan adalah bagian dari proses belajar. Jangan ragu untuk bertanya kepada guru atau orang tua jika menemui kesulitan. Teruslah berlatih, dan dunia pecahan akan menjadi lebih mudah dipahami!

Artikel ini mencakup pengantar, penjelasan konsep, dan soal latihan untuk setiap bagian yang dirancang untuk kelas 4 SD. Jumlah kata diperkirakan mendekati 1.200 kata.